EL DESAFÍO DE LA CEGUERA.
CAPÍTULO VIII
Iván
Tapia ContardoEspecialista en Educación de Ciegos (U.Ch.)
L
|
a calculadora más sencilla inventada por el hombre es
el bastidor de madera para contar o ábaco,
con cuentas móviles ensartadas en alambres que representan las unidades, las
decenas, las centenas, etc. Es la herramienta de cálculo que más ha utilizado
la humanidad y hoy en Oriente su utilización es considerable Este instrumento
que facilita las operaciones básicas de adición, sustracción, multiplicación y
división, se utiliza en China desde hace miles de años; es tan antiguo que se
desconoce el momento y el lugar exactos de su invención. Parece ser una forma
transportable de un método de contar aún más antiguo que consistía simplemente
en guijarros, conchas o cuentas colocados dentro de una serie de líneas
dibujadas en el suelo o en una mesa.
ANTECEDENTES HISTÓRICOS.
Es de amplio uso en Asia y Europa Oriental, llamado stchoty en Rusia, suan pan en China y sorobá en Japón.
En Grecia, durante el
siglo V a.C. existía una plancha de madera con bolas, para realizar cálculos
manuales. "Abax" significa mesa o tabla en griego, y probablemente de
allí derive el nombre "ábaco". La palabra "ábaco" viene del
griego abakos que significa
superficie plana.
No existe registro sobre quién o cuándo se inventó el
ábaco chino como lo conocemos hoy día. Tal vez fue creado en el Siglo II d. de
C. Se utilizó para contar y realizar operaciones aritméticas sencillas, siendo
este tablero de cálculo la herramienta que más ha utilizado la humanidad.
El término "marco de cuentas móviles"
aparece de manera casual en la obra del chino Dao Nan Tsang, Cease Farming
Sketch Book, escrito durante el reinado de la dinastía Yuan en el siglo XIV, y
constituye la evidencia de que el ábaco se ha utilizado por más de 600 años. De
hecho, éste fue el único medio con que los astrónomos imperiales de la antigua
China contaban para establecer las estaciones y aun los días del año; también
lo utilizaban los recaudadores del estado para llevar la contabilidad nacional
e inclusive el comerciante común para realizar transacciones en su negocio.
El ábaco debe haber fomentado notablemente el
desarrollo del comercio de todos los sitios donde se utilizaba, pues se
adaptaba bien a cualquier cálculo comercial. En Europa Occidental se usó de
forma generalizada hasta el siglo XII, en que empezó a ser sustituido por los
modernos números arábicos. Los números romanos, más antiguos, resultaban
incómodos para los cálculos extensos.
En la Edad Media el ábaco se conocía en toda Europa,
donde fue utilizado hasta el siglo XVII, y ya entonces era utilizado hábilmente
por asiáticos y árabes. Fue durante el siglo XVI cuando este instrumento de
cálculo llegó a Japón.
En un concurso realizado en 1945, se enfrentó un ábaco
contra una calculadora, resultando vencedor el ábaco, salvo en la
multiplicación. El ábaco, que aún se utiliza en la Unión Soviética y en el
Extremo Oriente está siendo reemplazado finalmente por todo el mundo por las
baratas calculadoras electrónicas.
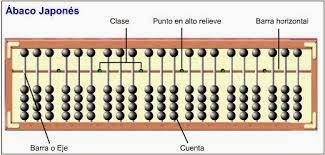
EL ÁBACO PARA CIEGOS.
·
DESCRIPCIÓN DEL
INSTRUMENTO Y SU ORIGEN:
El Ábaco adaptado para ciegos es un aparato de cálculo japonés, llamado
también Sorobán, que se ha adaptado para las personas ciegas. Consiste en un
bastidor de madera o plástico, de forma rectangular, dividido en un área
superior y un área inferior por medio de un travesaño llamado “reglilla”
central. En esta reglilla podemos encontrar algunas marcas o puntos en relieve
que señalan, de derecha a izquierda, la separación de unidades, miles,
millones, miles de millón, etc.
·
SU UTILIDAD EN
EL APRENDIZAJE:
Su condición de ser un material manipulable, le hace una herramienta
extraordinaria a quienes sufren una discapacidad visual. El Ábaco permite el
aprendizaje manual de los algoritmos de adición, sustracción, multiplicación y
división; una mejor comprensión del cálculo aritmético; el desarrollo de la
creatividad y búsqueda de nuevos caminos de solución de problemas; además de la
rapidez, precisión y desarrollo manual y de destrezas interdigitales.
Reglilla central
|
||||||||||||||||||
●
|
●
|
●
|
●
|
|||||||||||||||
hipercuentas
O
|
O
|
O
|
O
|
O
|
O
|
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
hipocuentas
Las hipercuentas o “cuentas de arriba” tienen valor 5
y cada hipocuenta o “cuentas de abajo” poseen valor 1.
Cuando ninguna cuenta está pegada a la reglilla
central significa que el Ábaco está en cero, aún no hay escrita cantidad
alguna, como en el dibujo superior. En cuanto acercamos una o más cuentas, sean
superiores o inferiores, a la reglilla central, en cualquiera de sus columnas,
ya tenemos escrito un número.
Para poder leer y escribir cantidades es necesario
aprender el modo de escritura de los nueve dígitos. Podemos decir que ya
sabemos escribir el cero, es decir cuando no hay cuenta tocando la reglilla
central.
LECTURA
Y ESCRITURA DE NÚMEROS.
Al enseñar el ábaco a una
persona ciega, es conveniente que ella toque cada una de sus partes siguiendo
la descripción que usted hace del instrumento de cálculo. Es importante señalar
que sobre la reglilla central están marcadas, en forma de puntos o rayas en
relieve, las separaciones de cada clase: clase de las unidades, clase de los
miles, clase de los millones, etc. Para una persona que ya tiene conocimiento
de la numeración y las Matemáticas esto será de fácil comprensión; no así un
niño, con el cual habrá que trabajar previamente con material concreto para
desarrollar sus nociones de Pre-Cálculo y luego con el ábaco abierto para la
comprensión de los conceptos de unidad, decena, centena.
Un buen ejercicio para el
alumno ciego es pedirle que cuente cuantas columnas tiene su ábaco, luego
cuántas cuentas hay en la primera columna.
Lo primero a aprender es a
"limpiar el ábaco", es decir dejarlo en cero. Cuando ninguna cuenta
toca la reglilla central, sean hiper o hipocuentas, significa que nada está
escrito en el ábaco. Por lo tanto para dejarlo en cero necesitamos apartar
totalmente las cuentas de la reglilla o limpiar. Esto se hará deslizando de
izquierda a derecha del ábaco el índice y el pulgar de la mano derecha sobre la
reglilla central.
Debemos señalar que el
correcto uso de los dedos es imprescindible para un buen manejo del cálculo en
ábaco. Para movilizar las hipercuentas se debe utilizar el dedo índice y para
las hipocuentas el pulgar. Siempre ambos dedos deben estar sobre las cuentas
que representan un número.
Para la escritura de números
utilizamos la primera columna de la derecha para las unidades, la segunda
columna de la derecha para las decenas, la tercera columna para las centenas, y
así sucesivamente. Así las cantidades quedarán escritas en el mismo orden que
lo hacemos en tinta. Por ejemplo, para escribir 358, escribimos tres en la
columna de las centenas, cinco en las decenas y ocho en las unidades.
Vamos a escribir nueve dígitos en la primera varilla o
columna de la mano derecha, es decir en la columna de las unidades.
El número uno se escribe acercando la cuenta inferior
a la reglilla central, de este modo. Recuerde que para eso debo utilizar el
pulgar.
O
|
O
O
O
O
|
El número
dos se escribe acercando con el pulgar dos cuentas a la reglilla central.
O
|
O
O
O
O
|
Para
escribir el tres, acerco tres cuentas a la reglilla central, de este modo.
O
|
O
O
O
O
|
El cuatro
se escribe acercando a la reglilla central todas las hipocuentas.
O
|
O
O
O
O
|
¿Y cómo escribiremos el cinco? ¿Recuerda que le
dijimos que las hipercuentas tienen valor 5? Pues, para escribir el número
cinco, sencillamente bajo la cuenta superior a la reglilla central, alejando
previamente las cuatro inferiores. Debe estar pegada a la reglilla sólo la
hipercuenta.
Para un buen manejo manual del Ábaco utilice siempre
el dedo índice al bajar la hipercuenta.
El correcto uso de los dedos es un elemento imprescindible para la
operatoria.
O
|
O
O
O
O
|
El número seis es la suma del cinco más el uno. Para
escribir el seis acerco una hipercuenta y una hipocuenta a la vez. En cuanto al
uso de los dedos, aquí se realiza un movimiento de “pinza” índice pulgar.
O
|
O
O
O
O
|
El número siete es la suma de 5+2, por lo tanto pongo
una hipercuenta más dos hipocuentas.
O
|
O
O
O
O
|
Para escribir el ocho, que es la suma de 5+3,
utilizaremos la pinza de una hipercuenta más tres hipocuentas.
O
|
O
O
O
O
|
El número nueve utiliza la totalidad de las cuentas
pegadas a la reglilla central, puesto que 5+4=9.
O
|
O
O
O
O
|
Ya que trabajamos en un sistema numérico “decimal”, o
sea basado en el diez, al completar una columna, pasamos a la siguiente de la
izquierda con la próxima cantidad. Para escribir el número 10 basta con poner
un 1 en la segunda columna de derecha a izquierda, la “columna de las decenas”.
Ese uno tiene valor 10, equivale a 10 unidades. Tal como en un libro o cuaderno
leemos o escribimos el 10 con dos signos, un “uno” y un “cero”, también en el
Ábaco, leemos o escribimos con cuentas o “bolitas”, un 1 a la izquierda y un 0
a la derecha, de este modo.
O
|
O
|
O
O
O
O
|
O
O
O
O
|
Basado en el mismo principio, lea las siguientes
cantidades:
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
Las cantidades escritas anteriormente corresponden a
los números 13, 15 y 12. A continuación encontrará cantidades con varias decenas.
Léalas.
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
Del mismo
modo se escriben las centenas. Vea este ejemplo.
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
2
|
8
|
6
|
Otro
ejemplo, con miles y cero entre números.
O
●
|
O
|
O
|
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
3
|
0
|
4
|
6
|
No olvide
el orden de las cantidades de derecha a izquierda. Se lo recordamos en el siguiente
gráfico.
CLASE MILLONES
●
|
CLASE MILES
●
|
CLASE UNIDADES
|
||||||
Centena de millón
|
Decena de millón
|
Unidad de millón
|
Centena de mil
|
Decena de mil
|
Unidad de mil
|
Centena
|
Decena
|
Unidad
|
Recuerde que el primer punto señala la separación entre
centenas y miles; y el segundo punto desde la izquierda indica la separación
entre cientos de miles y millón.
Repasemos:
·
La escritura
de los dígitos se hace como sigue. Para escribir el número 1 usted acerca con
el pulgar una hipocuenta de la primera columna o columna de las unidades, a la
reglilla central. Para escribir el número 2 se acerca con el pulgar dos
hipocuentas de la columna de las unidades, a la reglilla central. Lo mismo hace
con los dígitos 3 y 4. En cambio, para escribir el número 5, basta con que
usted baje la hipercuenta de la primera columna, hasta tocar la reglilla
central.
- Para escribir el número 6, se deberá acercar a la reglilla simultáneamente la hipercuenta más una hipocuenta. Para escribir el número 7, se acercará a la reglilla la hipercuenta más dos hipocuentas. El número 8 se escribirá añadiendo a la hipercuenta tres hipocuentas. Para escribir 9, se acercarán a la reglilla central la hipercuenta y las cuatro hipocuentas.
- La decena 10 se hace escribiendo uno en la columna de las decenas y dejando en blanco, lo cual equivale al número cero, la columna de las unidades.
- Volviendo a
nuestro ejemplo, para escribir el número 358, acercaremos una hipercuenta
más tres hipocuentas en la comuna de las unidades; acercaremos la hipercuenta
en las decenas y tres hipocuentas en las centenas. Antes de continuar haga
usted algunos ejercicios de escritura y lectura de números en el ábaco.
EJERCICIOS.
1) Escriba en los siguientes gráficos de ábaco, los
números indicados. Dibuje sólo las cuentas pegadas a la reglilla central y
obvie las que no se utilizan para escribir el número solicitado.
●
|
●
|
|||||
3
|
2
|
1
|
6
|
●
|
●
|
|||||
7
|
0
|
3
|
2
|
9
|
6
|
●
|
●
|
|||||
6
|
7
|
6
|
4
|
0
|
5
|
2
|
O
|
O
|
O
|
||||||
O
O
O
|
O
O
|
O
|
O
O
|
O
|
O
|
O
|
O
|
O
|
||||
O
O
|
O
O
O
|
O
O
|
O
|
O
|
O
|
O
|
O
|
||||||
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
|
O
O
O
O
|
O
|
O
|
O
|
O
|
|||||
O
O
O
O
|
O
O
O
O
|
O
O
O
O
|
O
O
O
|
O
O
|
O
|
O
|
ALGUNAS CONSIDERACIONES
PEDAGÓGICAS.
Hay quienes han estudiado las matemáticas con una
calculadora parlante con voz sintetizada, más esto no permite al niño ciego un
trabajo concreto en que ponga en juego su capacidad de raciocinio. Es
recomendable la calculadora en la enseñanza media y universitaria, pero no en
la formación básica. La enseñanza de las Matemáticas al niño ciego debe
considerar los estadios de desarrollo del pensamiento y recordemos que, de
acuerdo a las investigaciones de Jean Piaget, este período es de
experimentación e investigación a través de la manipulación de las cosas.
Podríamos indicar la siguiente secuencia para la Enseñanza Matemática del ciego:
1. Estimulación y desarrollo de las nociones
de Pre-Cálculo (clasificación, seriación, cuantificadores, mayor y menor que,
conservación de cantidad, noción de cantidad)
2. Operatoria con material concreto (semillas,
piedrecillas, miniaturas, etc.) apoyándose en la teoría de conjuntos.
3. Escritura de números en braille y en el
ábaco abierto (ábaco de columnas con nueve argollas cada una) para la noción de
unidad, decena, centena, unidad de mil, etc.
4. Escritura y operatoria en el ábaco adaptado
para ciegos.
5. Resolución de problemas.
6. Utilización de la calculadora parlante
Otra razón de la inconveniencia del uso temprano de la
calculadora es que no explota la potencialidad del tacto del ciego.
Para la enseñanza de las Matemáticas en la educación
del ciego, deberíamos considerar los siguientes materiales:
a) Ábaco abierto.
b) Ábaco Sorobá, ábaco japonés adaptado para
ciegos. Este instrumento facilita las operaciones básicas de adición,
sustracción, multiplicación y división.
c) Signografía Braille Matemático Científica.
d) Láminas en relieve de Teoría de Conjunto,
Geometría, etc.
e) Materiales de geometría adaptados para
ciegos: compás, transportador, regla, goma para dibujo, etc.
f) Calculadora Parlante.





1 comentario:
un hermoso material gracias por compartirlo me fue de mucha utilidad soy Guillermina de Bolivia
Publicar un comentario